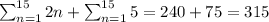Question

Find the sum of a finite arithmetic sequence from n = 1 to n = 15, using the expression 2n + 5

Answer 1

Assuming you mean the sequence is given explicitly by
`a_n=2n+5`, the sum of the first 15 terms is


`\displaystyle\sum_(n=1)^(15)a_n=\sum_(n=1)^(15)(2n+5)=2\sum_(n=1)^(15)n+5\sum_(n=1)^(15)1`

Recall Faulhaber's formulas, which say


`\displaystyle\sum_(n=1)^k1=k`

`\displaystyle\sum_(n=1)^kn=\frac{k(k+1)}2`

Our sum is then


`\displaystyle\sum_(n=1)^(15)a_n=2\frac{15*16}2+5*15=315`

Answer 2

`\sum _(n=1)^(15)2n+\sum _(n=1)^(15)5=240+75=315`

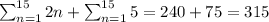
Explanation:

Given:
`\sum _(n=1)^(15)\:2n+5`

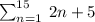
We have to calculate the sum of given expression.

Consider the given expression
`\sum _(n=1)^(15)\:2n+5`

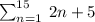
Apply sum rule,
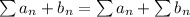`\sum a_n+b_n=\sum a_n+\sum b_n` , we get,

`=\sum _(n=1)^(15)2n+\sum _(n=1)^(15)5`

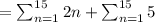
Now first consider
`\sum _(n=1)^(15)2n`

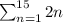
Using constant multiplication rule,
`\sum c\cdot a_n=c\cdot \sum a_n`

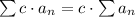
we have,

`=2\cdot \sum \:_(n=1)^(15)n`

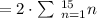
Apply sum formula,
`\sum _(k=1)^nk=(1)/(2)n\left(n+1\right)`

`=(1)/(2)\cdot \:15\left(15+1\right)=120\\\\ \sum _(n=1)^(15)2n=240`

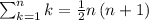
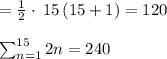
Now consider
`\sum _(n=1)^(15)5`

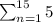
Apply sum formula,
`\sum _(k=1)^n\:a\:=\:a\cdot n`

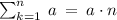
Here, a = 5 and n = 15

we get
`\sum _(n=1)^(15)5=75`

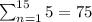
Therefore
`\sum _(n=1)^(15)2n+\sum _(n=1)^(15)5=240+75=315`