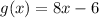Answer:
Shift 4 units down:

Stretching f(x) by 4 :
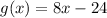
Shift 4 units left:

Compress by 1/4 units :
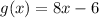
Explanation:
Given
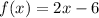
Required
Match the transformations (See attachment)
Shift 4 units down
Shifting down a function is represented as:
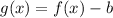
In this case:
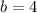
Substitute expression for f(x) and 4 for b in
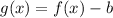
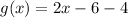

Stretching f(x) by 4
Stretching a function by some units is represented as:
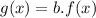
In this case:
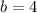
Substitute expression for f(x) and 4 for b in
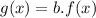
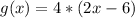
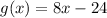
Shift 4 units left
Shifting a function to the left is represented as:
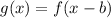
In this case:
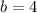
Substitute expression for f(x) and 4 for b in
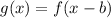
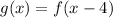
Calculating f(x - 4)
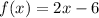
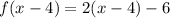

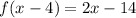
Hence:

Compress by 1/4 units
This means that the function is stretched by
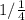
Compressing a function is represented as:
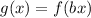
In this case:
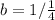
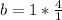
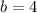
Substitute expression for f(x) and 4 for b in
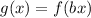
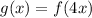
Calculating f(4x)
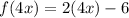
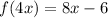
Hence: