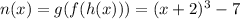Answer:
n(x) = g(f(h(x)))
Explanation:
Given
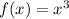
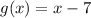
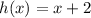
Required
Which function represents

Start by solving for f(h(x)):
Given that:
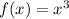 and
and
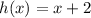
Substitute x + 2 for the x in f(x)
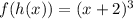
Next, solve for g(f(h(x)))
Given that:
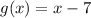 and
and
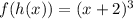
Substitute (x + 2)^3 for the x in g(x)

Recall that:

Hence: