Answer:
Answer : B
Explanation:
Our sequence is 3,-9,27,........This is a geometric sequence. whose first terms is 3 which is generally denoted by "a" .The common ratio is find out by taking the ration of second term to the first term. In this case it would be ,
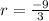
Hence r=-3
Now the formula for the nth term of any geometric sequence is given as
 =
=
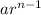
Hence we now replace the value of a and r in this to find the right answer which is
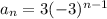
Hence B option is correct as the first term is not taken into the account in this answer.