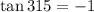Question

The measure of angle θ is 7π/4. The measure of its reference angle is __°, and tan θ is __.

Answer 1

The reference angle of 315 degree or
`(7\pi)/(4)` is 45 degrees.

`\tan 315=-1`

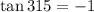
Explanation:

Given : The measure of angle
`\theta` is
`(7\pi)/(4)`.

To find : The measure of its reference angle is __°, and tan θ is __ ?

Solution :

The measure of angle
`\theta=(7\pi)/(4)`

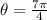
To get reference angle we convert radian into degree by multiplying
`(180)/(\pi)`

`\theta=(7\pi)/(4)* (180)/(\pi)`

`\theta=(7* 180)/(4)`

`\theta=315^\circ`

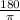
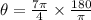
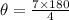
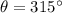
Reference angle is the angle between x-axis and the terminal side of given angle.

The terminal side of angle 315 is lying in 4th quadrant.

The angle between x-axis and its terminal side is 360-315 = 45 degrees

The reference angle of 315 degree or
`(7\pi)/(4)` is 45 degrees.

Now,
`\tan 315=\tan(360-45)`

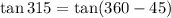
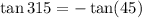`\tan 315=-\tan(45)` (tan is negative in 4th quadrant)

`\tan 315=-1`

Answer 2

7π/4

Is in the 4th forth quadrant so the reference angle can be solve using

A = 2π - 7π/4
A = π/4
Convert to degree
A = π/4 ( 180 degree/ π)
A = 45 degree

Tan(A) = tan (45) = 1