Answer:
Opposite interior angles of a parallelogram are congruent.
Explanation:
To answer this question let's do it step by step. So step
1) Consider the parallelogram GDEF
2) Trace a straight line, since two points define a line. Trace
 and another
and another
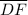
3) Consider these pair of parallel segments:
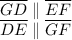
4) Now let's examine the angles. According to Euclides since DE and GF are parallels we can say that:
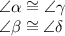
5) This step is the conclusion of the previous one, since alternate interior angles have the same measure, so
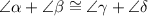
Opposite interior angles of a parallelogram are congruent.