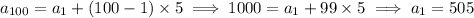Question

For the following arithmetic sequence, if d=5 and a_100=1000,what is a_1 ?

Answer 1

The nth term of an arithmetic sequence = a + (n - 1)d

a = 1st term = ? n =nth term = 100. d = common difference = 5

a₁₀₀ = a + (100 - 1)d

a₁₀₀ = a + 99d = 1000

a + 99d = 1000

a + 99*5 = 1000

a + 495 = 1000

a = 1000 - 495

a = 505

So the first term a, is the same as a₁ = 505

I hope this helped.

Answer 2

An arithmetic sequence has the recursive structure


`a_n=a_(n-1)+d`

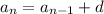
and can be solved explicitly for the
`n` term,
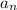
`a_n`, in terms of the first term of the sequence
`a_1`.


`a_n=a_(n-1)+d`

`\implies~a_n=a_(n-2)+2d`

`\implies~a_n=a_(n-3)+3d`

`\implies\cdots\implies a_n=a_1+(n-1)d`

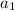
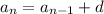
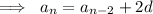
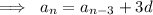
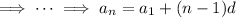
You know the 100th term of the sequence is
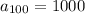
`a_(100)=1000` and that the common difference between terms is
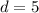
`d=5`, which means you have enough information to find the first term:


`a_(100)=a_1+(100-1)*5\implies1000=a_1+99*5\implies a_1=505`