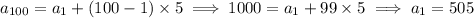An arithmetic sequence has the recursive structure
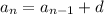
and can be solved explicitly for the

term,
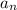
, in terms of the first term of the sequence
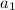
.
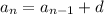

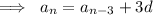
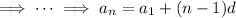
You know the 100th term of the sequence is
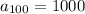
and that the common difference between terms is
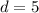
, which means you have enough information to find the first term: