Answer:
The recursive formula defines the sequence is
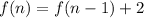 .
.
Explanation:
Three terms of an arithmetic sequence are
f(1) = 6
f(4) = 12
f(7) = 18
It means first term is 6, fourth term is 12 and seventh term is 18.
The formula for nth term of an arithmetic sequence is

where n is number of term, a is first term and d is common difference.
4th term of the AP is
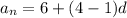
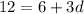
![[\because a_4=f(4)=12]](https://img.qammunity.org/2018/formulas/mathematics/middle-school/wd0nq3ziy608gcqo5t0iogdmikcsdm33ec.png)
Subtract 6 from both sides.
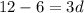
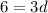
Divide both sides by 3.
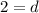
The common difference is 2.
The recursive formula for an AP is
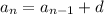
Substitute d=2 in the above equation.
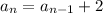
It can be written as
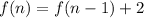
Therefore the recursive formula defines the sequence is
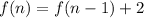 .
.