Answer:
Option C is correct
9 the simplified base for the given function f(x)
Explanation:
Using exponent rules:
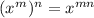
![\sqrt[n]{x^b} = x^{(b)/(n)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/s824zdxe2zaskv8yrmeagvchd5k32wa98p.png)
Given the function:
![f(x) = 2\sqrt[3]{27^(2x)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/co5e4c8677jhkf9ds872ivugx2p3oxtwnb.png)
We can write 27 as:
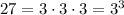
then;
![f(x) = 2\sqrt[3]{(3^3)^(2x)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/bo6zqv571w7pyy4pn4r4plml5vu9ccbuwf.png)
Apply the exponent rules:
![f(x) = 2\sqrt[3]{3^(6x)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/g37smelytuajnxsgqwarkzswzj8wgfpowh.png)
Apply the exponent rules:
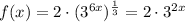
⇒
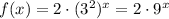
⇒
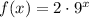
On comparing with exponential function
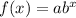 where, b is base of the exponent function, then
where, b is base of the exponent function, then
b = 9
Therefore, the simplified base for the given function is, 9