Answer:
b. X and Z
Explanation:
Since, the effective annual rate is,
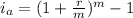
Where r is the nominal rate per period,
m is the number of periods in a year,
For loan X,
r = 7.815 % = 0.07815
m = 2,
Thus, the effective annual rate,
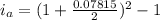
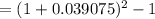
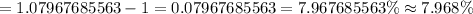
Since, 7.968\% < 8.000 %
Thus, Loan X meets his criteria.
For loan Y,
r = 7.724%= 0.07724
m = 12,
Thus, the effective annual rate,
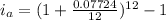
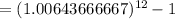
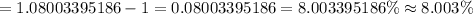
Since, 8.003 > 8.000 %
Thus, Loan Y does not meet his criteria.
For loan Z,
r = 7.698% = 0.07698
m = 52,
Thus, the effective annual rate,
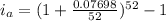
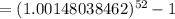
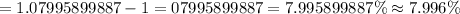
Since, 7.996 % < 8.000 %
Thus, Loan Z meets his criteria.
Hence, option 'b' is correct.