Question

Mike is looking for a loan. He is willing to pay no more than an effective rate of 8.000% annually. Which, if any, of the following loans meet Mike’s criteria?

Loan X: 7.815% nominal rate, compounded semiannually
Loan Y: 7.724% nominal rate, compounded monthly
Loan Z: 7.698% nominal rate, compounded weekly
a. Y only
b. X and Z
c. Y and Z
d. None of these meet Mike’s criteria.

Answer 1

X and Z

Explanation:

Answer 2

b. X and Z

Explanation:

Since, the effective annual rate is,

`i_a=(1+(r)/(m))^m-1`

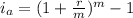
Where r is the nominal rate per period,

m is the number of periods in a year,

For loan X,

r = 7.815 % = 0.07815

m = 2,

Thus, the effective annual rate,

`i_a=(1+(0.07815)/(2))^2-1`

`=(1+0.039075)^2-1`

`=1.07967685563-1=0.07967685563=7.967685563\% \approx 7.968\%`

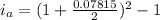
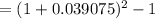
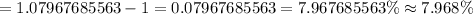
Since, 7.968\% < 8.000 %

Thus, Loan X meets his criteria.

For loan Y,

r = 7.724%= 0.07724

m = 12,

Thus, the effective annual rate,

`i_a=(1+(0.07724)/(12))^(12)-1`

`=(1.00643666667)^(12)-1`

`=1.08003395186-1=0.08003395186=8.003395186\% \approx 8.003\%`

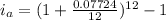
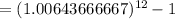
Since, 8.003 > 8.000 %

Thus, Loan Y does not meet his criteria.

For loan Z,

r = 7.698% = 0.07698

m = 52,

Thus, the effective annual rate,

`i_a=(1+(0.07698)/(52))^(52)-1`

`=(1.00148038462)^(52)-1`

`=1.07995899887-1=07995899887=7.995899887\% \approx 7.996\%`

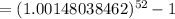
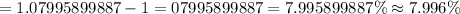
Since, 7.996 % < 8.000 %

Thus, Loan Z meets his criteria.

Hence, option 'b' is correct.