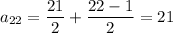Question

Aye can u help me? :)

Given the following sequence, find the 22nd term:

10.5, 11, 11.5, 12, 12.5, . . .

A. 20.5
B. 21
C. 21.5
D. 22

Answer 1

the answer is B.

Explanation:

Answer 2

The given sequence is arithmetic with a common difference of
`\frac12` between each term.

Recursively, you can define the sequence as


`a_n=a_(n-1)+\frac12`

and solve explicitly for the
`n`th term by recursively substituting the right hand side:


`a_n=a_(n-1)+\frac12`

`\implies~a_n=a_(n-2)+2*\frac12`

`\implies~a_n=a_(n-3)+3*\frac12`

`\implies\cdots\implies~a_n=a_1+(n-1)\frac12`

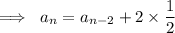
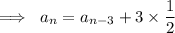
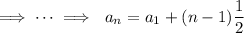
The first term of the sequence is
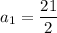
`a_1=\frac{21}2`, so the
`n`th term is given by the formula


`a_n=\frac{21}2+\frac{n-1}2`

So, the 22nd term in the sequence is


`a_(22)=\frac{21}2+\frac{22-1}2=21`