Question

F(x)=-x^3+24x^2-179x+495 determine the
Average rate of change of f(x) between x=2 and x=5

Answer 1

The average rate of change is -75

Explanation:

The Average Rate of Change (ARC)

It's a measure of how much the function changed per unit, over a given interval.

Given a function F(x) and an interval between x=a and x=b, the average rate of change is:

`\displaystyle A=(F(b)-F(a))/(b-a)`

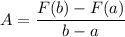
The function is:

`F(x)=-x^3+24x^2-179x+495`

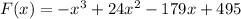
and it's required to find the ARC between x=2 and x=5.

Calculate F(2) and F(5):

`F(2)=-2^3+24*2^2-179*2+495=225`

`F(5)=-5^3+24*5^2-179*5+495=75`

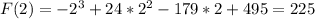
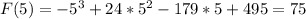
The ARC is:

`\displaystyle A=(75-225)/(5-3)=(-150)/(2)=-75`

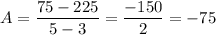
The average rate of change is -75