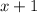Answer:
Explanation:
A slant (oblique) asymptote occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.
To find the slant asymptote you must divide the numerator by the denominator using either long division or synthetic division.
We are given a function:
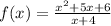
Since in the given function the polynomial in the numerator is a higher degree than the polynomial in the denominator.
So, now to find oblique asymptote we will divide the numerator by the denominator
So, on dividing we get :
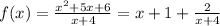 j
j
Now, As
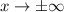 the remainder term disappears
the remainder term disappears
So the oblique asymptote is the line
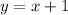
Thus, the oblique asymptote of the function
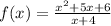 is
is