Answer: 55 miles per hour
Explanation:
Given : The graph shows the distance, y, that a car traveled in x hours.
The rate of change of a function is given by :-

When we look in the graph , we observe that the graph is passing through two points (0,0) and (1,55).
Now, the rate of change for the relationship represented in the graph will be :_
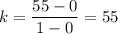
Hence, the rate of change for the relationship represented in the graph is 55 miles per hour.