Question

5x + 3y = 38
2x+3y=13
y=?
x=?

Answer 1

The solution to the system of equations is:

`x=(25)/(3),\:y=-(11)/(9)`

Explanation:

Given the system of equations

`5x + 3y = 38`

`2x + 3y = 13`

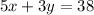
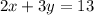
solving the system of equations

`\begin{bmatrix}5x+3y=38\\ 2x+3y=13\end{bmatrix}`

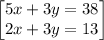
Multiply 5x+3y=38 by 2: 10x+6y=76

Multiply 2x+3y=13 by 5: 10x+15y=65

`\begin{bmatrix}10x+6y=76\\ 10x+15y=65\end{bmatrix}`

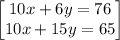
so

`10x+15y=65`

`-`

`\underline{10x+6y=76}`

`9y=-11`

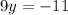
now solving 9y = -11 for y

`9y=-11`

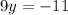
divide both sides by 9

`(9y)/(9)=(-11)/(9)`

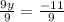
Simplify

`y=-(11)/(9)`

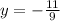
For 10x+6y=76 plug in y = -11/9

`10x+6\left(-(11)/(9)\right)=76`

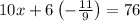
subtract 6(-11/9) from both sides

`10x+6\left(-(11)/(9)\right)-6\left(-(11)/(9)\right)=76-6\left(-(11)/(9)\right)`

`10x=(250)/(3)`

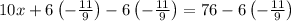
Divide both sides by 10

`(10x)/(10)=((250)/(3))/(10)`

`x=(25)/(3)`

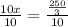
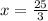
Therefore, the solution to the system of equations is:

`x=(25)/(3),\:y=-(11)/(9)`