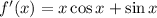Question

Derivative of xsinx by using first principle

Answer 1

Let
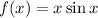
`f(x)=x\sin x`. Then the derivative is given by the limit


`f'(x)=\displaystyle\lim_(h\to0)\frac{f(x+h)-f(x)}h=\lim_(h\to0)\frac{(x+h)\sin(x+h)-x\sin x}h`

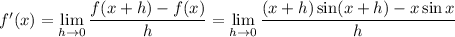
Expand the numerator:


`(x+h)\sin(x+h)-x\sin x=x(\sin x\cos h+\sin h\cos x)+h(\sin x\cos h+\sin h\cos x)-x\sin x`

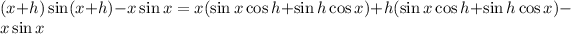
This can be rewritten as


`x\sin x(\cos h-1)+x\cos x\sin h+h(\sin x\cos h+\sin h\cos x)`

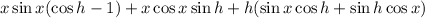
So you're left with the limit


`\displaystyle\lim_(h\to0)\frac{x\sin x(\cos h-1)+x\cos x\sin h+h(\sin x\cos h+\sin h\cos x)}h`

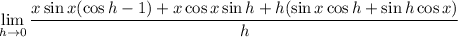
which you can split up as a sum of factored limits


`\displaystyle x\sin x\lim_(h\to0)\frac{\cos h-1}h+x\cos x\lim_(h\to0)\frac{\sin h}h+\lim_(h\to0)\frac{h(\sin x\cos h+\sin h\cos x)}h`

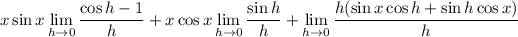
The first two limits use two special limits,


`\displaystyle\lim_(h\to0)\frac{1-\cos h}h=0\quad\text{and}\quad\lim_(h\to0)\frac{\sin h}h=1`

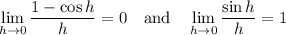
while for the last, you can cancel out the factors of
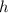
`h` in the numerator and denominator. You're left with


`\displaystyle 0+x\cos x+\lim_(h\to0)(\sin x\cos h+\sin h\cos x)`

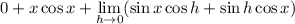
You have
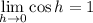
`\lim\limits_(h\to0)\cos h=1` and
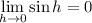
`\lim\limits_(h\to0)\sin h=0`, so the derivative is


`f'(x)=x\cos x+\sin x`