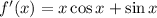Let
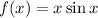
. Then the derivative is given by the limit
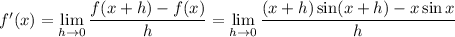
Expand the numerator:
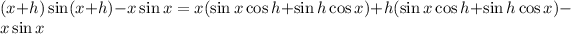
This can be rewritten as
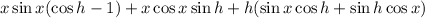
So you're left with the limit
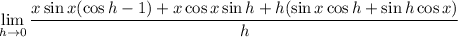
which you can split up as a sum of factored limits
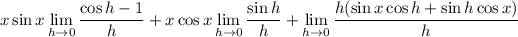
The first two limits use two special limits,
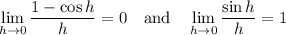
while for the last, you can cancel out the factors of
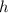
in the numerator and denominator. You're left with
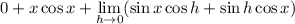
You have
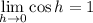
and
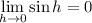
, so the derivative is