I don't know how to do it except for with deritivies
so take the deritivieve and find where the deritivieve equals 0
that is where the sign changes
where the sign changes from (+) to (-), that is max
so
A.
max revenue
R'(x)=
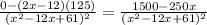
find where numerator is 0
at x=6
to find change of sign, evaluate the denomenator at above and below 6 and see sign
R'(5)=(+)
R'(7)=(-)
at x=6, the sign changes from (+) to (-)
max is at x=6
sub 6 for x in the R(x) function
R(6)=9 (it's in thousands so $9000 is te max revenue)
B.
max profit
combine them
P(x)=R(x)-E(x)
take the deritive of P(x)
using sum rule
P'(x)=R'(x)-E'(x)
we already know what R'(x) is
E'(x)=
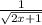
P'(x)=
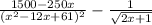
find zeroes or what value of x make P'(x) equal to 0
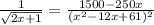
use calculator or something or work it out to find x
at x=5.225
x is hundreds so times 100
522.5
about 523 items
A. $9000
B. 523 items