Suppose

is a random variable representing student GPAs. Then

is normally distributed with mean 2.9 and standard deviation 0.5, so you have
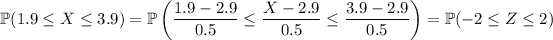
where
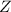
is a random variable also representing student GPAs, but follows the standard normal distribution with mean 0 and standard deviation 1.
The proportion of students with GPA between 1.9 and 3.9 is then equivalent to the proportion of the distribution that lies within two standard deviations of the mean. If you know the empirical rule (aka the 68-95-99.7 rule) then you should already know that
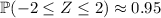
.
Otherwise you could consult a table of

scores to find the same (perhaps more accurate) probability.