Fix the first digit to be 2. How many two-digit descending numbers can you make? Only one, and that would be
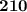
.
Now fix the first digit to be 3. How many two-digit descending numbers can you make? There are three, and these are
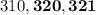
.
Next, if the first digit is 4, then there are six possible descending numbers,
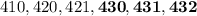
.
You might start seeing a pattern here. If the first digit is

, then each choice of

from
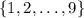
contributes

more possible two-digit permutations that are descending.
As the pattern continues, you'll find that the total number of descending three-digit numbers is

Meanwhile, there are

possible three-digit numbers that can be randomly chosen (100 through 999), so the probability you're looking for is
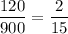
.