Answer:
9.42cm^3/s
Explanation:
The surface area of a sphere is decreasing at the constant rate of 3*pi sq. cm/sec . ? At what rate is the volume of the sphere decreasing at the instant its radius is 2 cm ?
We know a sphere has a volume and area
V=4/3
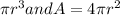
dA/dt=dA/dr*dr/dt............1
also dV/dt=dV/dr*dr/dt... ........
from equation 1
we can make dr/dt the subject of the equation
dr/dt=dA/dt/(dA/dr)
substitute into equation 2
dV/dt=dV/dr*(dA/dt/(dA/dr))
dv/dr=
 =4*3.14*2^2=50.24
=4*3.14*2^2=50.24
dA/dt= 3*pi
dA/dr=8*p1*2=
3/16*50.24
dV/dt=9.42cm^3/s
is the rate at which the volume is decreasing