Question

Mary deposited $350 in a bank account that promises 2.8 percent interest compounded continuously. Approximately how many years will it take to reach a balance of $500?

Answer 1

You use the formula
A= Pe^rt for continuously compounded interest.
500=350e^(.028*t)
Divide both sides by 350
(10/7)=e^(.028t)
Take the natural log of both sides to clear the e.
Ln (10/7)=.028t
Divide both sides by .028
Ln (10/7)/.028 =t
12.75 years

Answer 2

The time taken to reach the balance is approximately 13 years.

Explanation:

Given : Mary deposited $350 in a bank account that promises 2.8 percent interest compounded continuously.

To find : How many years will it take to reach a balance of $500?

Solution :

The formula of compounded continuously is

`A=Pe^(rt)`

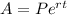
Where, A is the amount A=$500

P is the principal P=$350

r is the interest rate r=2.8%=0.028

t is the time in year.

Substitute the values in the formula,

`500=350* e^(0.028* t)`

`(500)/(350)=e^(0.028* t)`

`1.42=e^(0.028* t)`

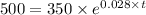
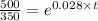
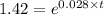
Taking log both side,

`\ln 1.42=0.028* t`

`0.356=0.028* t`

`t=(0.356)/(0.028)`

`t=12.71`

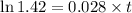
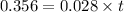
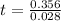
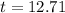
The time taken to reach the balance is approximately 13 years.