Step 1. Calculate the discriminant:
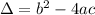
Step 2.
If
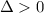
, there are two solutions, both real numbers
If

, there is only one solution, real number
If

, there are two solutions, both complex numbers
In your case:
a=3, b=6, c=4

So you have two solutions, both complex numbers