Answer:
Rate of change = -7
Initial value = 27
Explanation:
It is given that a linear function starting at point e(0, 27) and ending at point f(5,−8).
We need to find the rate of change for the linear function and its initial value.
If a linear function passes through two points then the rate of change is

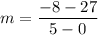
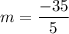
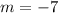
The rate of change for the linear function is -7.
The initial value of a function is its y-intercept, where x=0.
From the given points it is clear that the value of function is 27 at x=0.
Therefore, the initial value is 27.