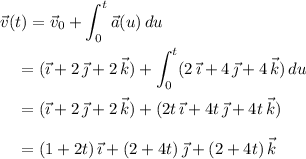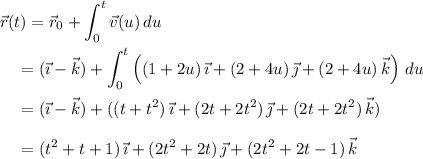Question

A particle traveling in a straight line is located at the point (1, 0, −1) and has speed 3 at time t = 0. the particle moves toward the point (3, 4, 3) with constant acceleration 2i+ 4j+ 4k. find the velocity v(t) and the position r(t) of the particle at time t.

Answer 1

We first observe that the particle moves in the direction of the vector

`(3\,\vec\imath + 4\,\vec\jmath + 3\,\vec k) - (\vec\imath - \vec k) = 2\,\vec\imath + 4\,\vec\jmath + 4\,\vec k`

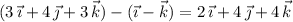
so the initial velocity vector
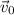`\vec v_0` is parallel to this vector. Given its initial speed is 3 at
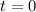`t=0`, this means for some scalar constant
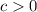`c>0`, we have

`\vec v_0 =  2c\,\vec\imath + 4c\,\vec\jmath + 4c\,\vec k`

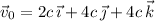
such that

`\|\vec v_0\| = √((2c)^2 + (4c)^2 + (4c)^2) = 6c = 3 \implies c = \frac12`

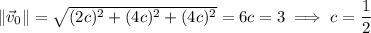
so that the initial velocity is

`\vec v_0 = \vec\imath + 2\,\vec\jmath + 2\,\vec k`

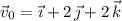
Now, use the fundamental theorem of calculus to compute the velocity and position functions.

`\displaystyle \vec v(t) = \vec v_0 + \int_0^t \vec a(u) \, du \\\\ ~~~~ = (\vec\imath + 2\,\vec\jmath + 2\,\vec k) + \int_0^t (2\,\vec\imath + 4\,\vec\jmath+4\,\vec k) \, du \\\\ ~~~~ = (\vec\imath + 2\,\vec\jmath + 2\,\vec k) + (2t\,\vec\imath + 4t\,\vec\jmath+4t\,\vec k) \\\\ ~~~~ = (1 +2t)\,\vec\imath + (2+4t)\,\vec\jmath + (2+4t)\,\vec k`

`\displaystyle \vec r(t) = \vec r_0 + \int_0^t \vec v(u) \, du \\\\ ~~~~ = (\vec\imath - \vec k) + \int_0^t \left((1 +2u)\,\vec\imath + (2+4u)\,\vec\jmath + (2+4u)\,\vec k\right) \, du \\\\ ~~~~ = (\vec\imath - \vec k) + ((t+t^2)\,\vec\imath + (2t+2t^2)\,\vec\jmath + (2t+2t^2)\,\vec k) \\\\ ~~~~ = (t^2+t+1)\,\vec\imath + (2t^2+2t)\,\vec\jmath + (2t^2+2t-1)\,\vec k`