Question

-GEOMETRY PROBLEM- I don’t understand this problem can anyone please help me? The problem is in the picture below. I will be giving 15 points! Thanks!

Answer 1

`\triangle \text{SAT} \cong \triangle \underline{ \ \ \textbf{SAO} \ }\text{ by } \underline{ \ \ \textbf{SAS}\ \ }`

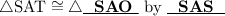
SAS = side angle side

========================================================

Step-by-step explanation:

It's probably visually apparent that one triangle is a mirror copy of the other. The mirror line is the segment SA.

So the triangles are congruent, but how do we fill in the first box? The order of the letters matters. This is because the order tells us how the letters pair up (which pieces are congruent to what).

The notation
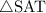`\triangle \text{SAT}` has "S" first then "A" next in that order.

So the answer will have that exact sequence of "S" then followed by "A". The only difference is that instead of "T", we go for point "O".

When writing
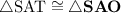`\triangle \text{SAT} \cong \triangle \textbf{SAO}` we have these corresponding angle pieces

• angle S = angle S
• angle A = angle A
• angle T = angle O

It might seem silly to repeat angles like this, but it's still handy to do anyway.

Based on those angle pairings, we can then say

• side SA = side SA
• side AT = side AO
• side OS = side TS

Again, the order helps us see which sides are congruent even if we didn't have a diagram handy.

So for instance, an incorrect response would be
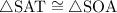`\triangle \text{SAT} \cong \triangle \text{SOA}` simply because the second letters "A" and "O" of each sequence do not match up.

---------------------

We can prove that
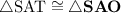`\triangle \text{SAT} \cong \triangle \textbf{SAO}` through the use of the SAS congruence theorem. Or just "SAS" for short.

SAS = side angle side

• The first "S" of "SAS" refers to the pairing that SA = SA, i.e. the overlapping shared sides between the two triangles.
• The second "S" is OS = TS due to the tickmarks shown.
• Then the "A" of "SAS" refers to the angles between the mentioned sides.

So that's why we're able to use SAS.