Answer:
The function N(t) is given as:
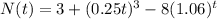
Explanation:
Jenny studied the characteristics of two species of bacteria.
The number of bacteria of species A, A(t), after t hours is represented by the function:
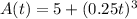
The number of bacteria of species B, B(t), after t hours is represented by the function:
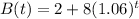
N(t) denotes the difference in the number of bacteria; hence N(t) is given by after t hours as:
N(t)=A(t)-B(t)
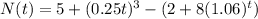
which on simplifying gives:
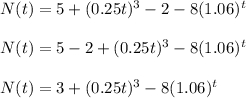
Hence,