A) Consider the equation
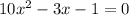
We have to describe the solutions to this equation.
We will determine the radicand =
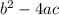
=
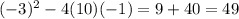 which is greater than zero,
which is greater than zero,
Therefore, the given equation ha real roots.
B) Consider the equation
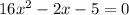
We will use middle splitting term method to solve this equation.
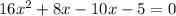
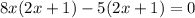

So,
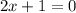
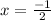 and
and
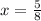
I chose this method, because this is more easier and takes less time.