Question

Write in slope-intercept form an equation of the line that passes through the given points.

(−1, −1), (1, 5)

Answer 1

Answer: y=3x+2

Step-by-step explanation:

Slope-intercept form: →
`y=mx+b`

m: represents the slope and is constant.

b: represents the y-intercept.

The y-intercept is the point on a graph at which the graph crosses the y-axis.

Used rise/run.

`m=(rise)/(run)`

`rise=y^2-y^1`

`run=x^2-x^1`

`(x^1,y^1)=(-1,-1)`

`(x^2,y^2)=(1,5)`

`rise=y^2-y^1=5-(-1)`

`run=x^2-x^1=1-(-1)`

`(5-(-1))/(1-(-1))= (6)/(2)=3*2=6=3`

`5-3(1)=2(1)=2*1=2`

Hope this helps!

Thanks!

Answer 2

Slope-intercept form uses the following equation: y = mx + b. m is the slope, and b is the y-intercept of the equation.

Use the following formula to figure out the rise and run of these points:


`(y2 - y1)/(x2 - x1)`

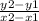
Plug the x and y values into the equation to determine the slope.


`(5 - (-1))/(1 - (-1))` =
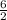
`(6)/(2)` = 3

Use the slope to find the y-intercept of the equation. You can find this by taking a point and using addition/subtraction and multiplication.

Taking the point (1,5), you can do the following:

5 - 3(1) = 2

The final equation is y = 3x + 2.