Answer:
The given equations are perpendicular as their slopes are negative reciprocals.
Explanation:
Given equations:
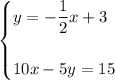
Rearrange the second question to isolate y:
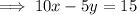
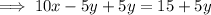
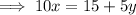
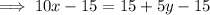
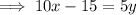
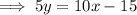
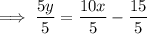
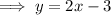

Therefore:
- The slope of the first equation is -¹/₂.
- The slope of the second equation is 2.
The slopes of parallel lines are the same.
The slopes of perpendicular lines are negative reciprocals.
The reciprocal of a number is 1 divided by the number.
Therefore, the negative reciprocal of 2 is -¹/₂.
The given equations are perpendicular as their slopes are negative reciprocals.