Answer:
The critical points are 2,-2 and -3.
Explanation:
Given the inequality
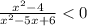
we have to find the critical points for the inequality
We reduce the given inequality into factored form
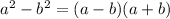
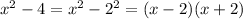
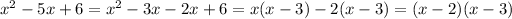
The inequality becomes
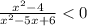
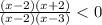
Critical points are those values of domain where it is not differentiable or its derivative is 0 or we can say the values at which the numerator and denominator is equal to zero.
Hence, the critical points are 2,-2 and -3.