Question

What are the critical points for the inequality x^2-4/x^2-5x+6<0?

Answer 1

X=-2, x=2, and x=3 these are the critical points

Answer 2

The critical points are 2,-2 and -3.

Explanation:

Given the inequality

`(x^2-4)/(x^2-5x+6)<0`

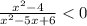
we have to find the critical points for the inequality

We reduce the given inequality into factored form

`a^2-b^2=(a-b)(a+b)`

`x^2-4=x^2-2^2=(x-2)(x+2)`

`x^2-5x+6=x^2-3x-2x+6=x(x-3)-2(x-3)=(x-2)(x-3)`

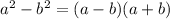
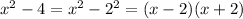
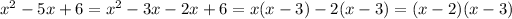
The inequality becomes

`(x^2-4)/(x^2-5x+6)<0`

`((x-2)(x+2))/((x-2)(x-3))<0`

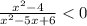
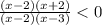
Critical points are those values of domain where it is not differentiable or its derivative is 0 or we can say the values at which the numerator and denominator is equal to zero.

Hence, the critical points are 2,-2 and -3.