Hi there! The answer is C. h = 6 or h = −7
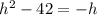
Add h to both sides of the equation.
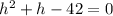
First we need to find the discriminant (which can be found using the formula D = b^2 - 4ac)
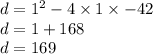
Now we can plug in our found values into the quadratic formula.
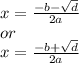
Plug in.
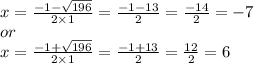
Hence, the answer is C. h = 6 or h = −7