Question

Triangles ABC and DEF are similar. The ratio of the side lengths in triangle ABC to triangle DEF is 1:3. If the area of triangle ABC is 1 square unit, what is the area of triangle DEF?

Answer 1

Triangles ABC and DEF are similar. The ratio of the side lengths in triangle ABC to triangle DEF is 1:3. If the area of triangle ABC is 1 square unit, what is the area of triangle DEF?

Answer 2

The area of triangle DEF is 9 square units.

Explanation:

It is given that triangle ABC and DEF are similar and the ratio of the side lengths in triangle ABC to triangle DEF is 1:3.

Let the length of their sides be x and x respectively.

If two triangles are similar then the ratio of their areas is equal to the square of the ratio of their sides.

Since triangle ABC and DEF are similar, therefore

`(Area(ABC))/(Area(DE F))=((x)^2)/((3x)^2)`

`(1)/(Area(DE F))=((x)^2)/(9(x)^2)`

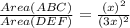
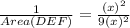
Cancel out the common factors.

`(1)/(Area(DE F))=(1)/(9)`

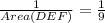
On cross multiplication, we get

`1* 9=1* Area(DE F)}`

`9=Area(DE F)}`

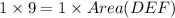
Therefore the area of triangle DEF is 9 square units.