Answer:
The area of triangle DEF is 9 square units.
Explanation:
It is given that triangle ABC and DEF are similar and the ratio of the side lengths in triangle ABC to triangle DEF is 1:3.
Let the length of their sides be x and x respectively.
If two triangles are similar then the ratio of their areas is equal to the square of the ratio of their sides.
Since triangle ABC and DEF are similar, therefore
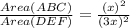
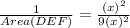
Cancel out the common factors.

On cross multiplication, we get
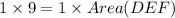

Therefore the area of triangle DEF is 9 square units.