Question

Identify the sequence graphed below and the average rate of change from n = 0 to n = 3.

coordinate plane showing the point 2, 10
point 3, 5
point 4, 2.5
and point 5, 1.25


an = 8(one half)n − 2; average rate of change is −3
an = 10(one half)n − 2; average rate of change is negative thirty five thirds
an = 8(one half)n − 2; average rate of change is 3
an = 10(one half)n − 2; average rate of change is thirty five thirds

Answer 1

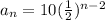`a_n=10((1)/(2))^(n-2)`; average rate of change is -35/3.

Explanation:

The graph of a sequence has points plotted using the term number as the x-coordinate and the term value as the y-coordinate.

This means the second term of the sequence is 10; the third term is 5; the fourth is 2.5; and the fifth is 1.25.

Looking at the term values, we see that 5 is half of 10; 2.5 is half of 5; and 1.25 is half of 2.5. This means that the common ratio, or constant that the sequence is multiplied by, is 1/2.

We start at the second term; this means the first term we are given, 10, is the second term of the sequence. For this reason, we will use (n-2) as our exponent (using 2 for the second term, we would have an exponent of 0; raising 1/2 to an exponent of 0 gives us the value 1, which will in turn keep our sequence at 10). This gives us

`a_n=10((1)/(2))^(n-2)`.

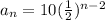Since the term values decrease every time, the rate of change will be negative. Our two options are positive 35/3 or -35/3; the correct choice will be -35/3.

Answer 2

For those who are looking for the answer, i just did the test, and got this question right. The answer is the second option: an = 10(1/2)n − 2; average rate of change is negative thirty five thirds. Hope this helps you all, and good luck.