Answer:
All integers where n ≥ 1
Explanation:
Given :
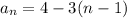
To find: Domain for n
Solution:
Arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant. Difference here means the second minus the first.
In arithmetic sequence,
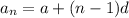
where a is first term.
d is common difference.
n is number of terms which belongs to natural numbers
And according to the definition of Arithmetic sequence n starts with 1
And we also know that natural number starts with 1
Now, in given sequence for nth term :
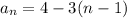
The domain for n is All integers where n ≥ 1