Question

Which is the equation of an ellipse centered at the origin with vertices (8,0) and (-8,0) and a minor axis length of 8?

Answer 1

the standard form of an ellipse with horizontal major axis as in this problem is:

`( x^(2) )/( a^(2) ) + ( y^(2) )/( b^(2) ) =1` where
"a" is greater than "b"

the major axis is length of 16 which means a = 8 and the minor axis length is 8 which means b = 4

the equation then is: Choice B

Answer 2

OptionB is right

Explanation:

Given that an ellipse centered at the origin with vertices (8,0) and (-8,0) and a minor axis length of 8

Since centre is at the origin, its equation would be of the form

`(x^2)/(a^2)+(y^2)/(b^2)=1`

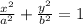
Since vertices are (8,0) and (-8,0) we find that a=8

Minor axis length = 2b =8 (given)

So b =4

The equation of the ellipse would be

`(x^2)/(8^2)+(y^2)/(4^2)=1\\(x^2)/(64)+(y^2)/(16)=1`

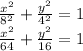
Option B is the right answer