Question

A tree casts a 25m shadow when the angle of elevation to the sun is 40. Approximately how tall is the tree?

Answer 1

check the picture below.

make sure your calculator is in Degree mode.

Answer 2

Approximately 20.98 meters tall.

Explanation:

We have been that a tree casts a 25 m shadow when the angle of elevation to the sun is 40 degrees. We are asked to find the height of the tree.

First of all, we will draw a graph to represent the given scenario.

The shadow of tree will form a right triangle with respect to tree and angle of elevation with ground as shown in the image.

We know that tangent relates opposite side of a right triangle with adjacent.

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(40^(\circ))=(h)/(25)`

`(h)/(25)=\text{tan}(40^(\circ))`

`(h)/(25)\cdot 25=\text{tan}(40^(\circ))\cdot 25`

`h=(0.839099631177)\cdot 25`

`h=20.977490779425`

`h\approx 20.98`

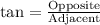
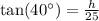
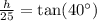
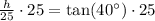
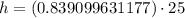
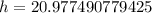
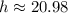
Therefore, the tree is approximately 20.98 meters tall.