Answer:
Approximately 20.98 meters tall.
Explanation:
We have been that a tree casts a 25 m shadow when the angle of elevation to the sun is 40 degrees. We are asked to find the height of the tree.
First of all, we will draw a graph to represent the given scenario.
The shadow of tree will form a right triangle with respect to tree and angle of elevation with ground as shown in the image.
We know that tangent relates opposite side of a right triangle with adjacent.
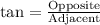
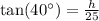
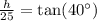
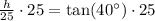
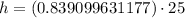
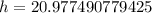
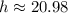
Therefore, the tree is approximately 20.98 meters tall.