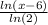Question

What is inverse function for f(x) =2^x+6

Answer 1

Ans: The inverse of the function is =
`f^(-1)(x)` =
`(ln(x-6))/(ln(2))`

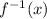
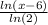Step-by-step explanation:
Given function:
f(x) = 2^x + 6

Step 1:
We can write f(x) as y:
y = 2^x + 6

Step 2:
Interchange x with y and vice versa:
x = 2^y + 6

Step 3:
Now solve for y:
x - 6 = 2^y

Take "ln" (natural log) on both sides:
ln(x-6) = ln(2^y)
ln(x-6) = yln(2)

y =
`(ln(x-6))/(ln(2))`

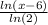
Step 4:
Now replace y with
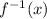
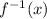
`f^(-1)(x)`:


`f^(-1)(x)` =
`(ln(x-6))/(ln(2))`