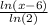Ans: The inverse of the function is =
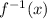
=
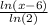 Step-by-step explanation:
Step-by-step explanation:Given function:
f(x) = 2^x + 6
Step 1:
We can write f(x) as y:
y = 2^x + 6
Step 2:
Interchange x with y and vice versa:
x = 2^y + 6
Step 3:
Now solve for y:
x - 6 = 2^y
Take "ln" (natural log) on both sides:
ln(x-6) = ln(2^y)
ln(x-6) = yln(2)
y =
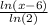
Step 4:
Now replace y with
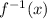
:
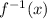
=