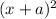To solve this we are going to use the special product for a binomial squared:
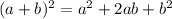
.
Notice that the term in the middle of our right side (
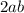
) is two times the multiplication of the square roots of the first term
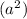
and the last term (
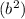
So, to simplify our expression we are going to apply the same. Since the term in the middle is two times the multiplication of the square roots of the first term
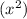
and the last term (
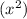
, the factored form of our expression will be
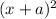
We can conclude that the factored form of
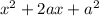
is