Question

Find the height h of the parallelogram.

Answer 1

tangent (angle theta) = 2.7 / 2.381 = 1.1339773205
arc tangent (1.11339773205) = 48.592 Degrees
cosine (48.592 ) = hgt / 1.5
height = 0.66142 * 1.5
height = 0.99213

Answer 2

B. 1.125 units.

Explanation:

We have been given a parallelogram and we are asked to find the horizontal height of our given parallelogram.

We will use area formula of parallelogram.

`\text{Area of parallelogram}=\text{Base* Height}`

We can find the area of our given parallelogram by taking 1.5 as base and 2.7 as height or we can take 3.6 as base and h as height.

Since areas found by both ways will be same so we can equate areas as:

`3.6*h=1.5*2.7`

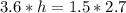
Let us solve for h by dividing both sides of our equation by 3.6.

`(3.6*h)/(3.6)=(1.5*2.7)/(3.6)`

`h=(4.05)/(3.6)`

`h=1.125`

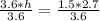
Therefore, the height h of parallelogram will be 1.125 units and option B is the correct choice.