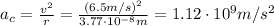Question

What is the acceleration of a proton moving with a speed of 6.5 m/s at right angles to a magnetic field of 1.8 t ?

Answer 1

The magnetic force acting on the proton is

`F=qvB \sin \theta`
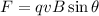
where
q is the proton charge
v is its speed
B is the intensity of the magnetic field

`\theta` is the angle between the direction of v and B; since the proton is moving perpendicular to the magnetic field,
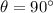
`\theta=90^(\circ)` and
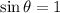
`\sin \theta=1`, so the force becomes

`F=qvB`

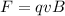
this force provides the centripetal force that keeps the proton in circular motion:

`m (v^2)/(r) = q v B`
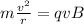
where the term on the left is the centripetal force, with
m being the mass of the proton
r the radius of its orbit

Re-arranging the previous equation, we can find the radius of the proton's orbit:

`r= (mv)/(qB)= ((1.67 \cdot 10^(-27) kg)(6.5 m/s))/((1.6 \cdot 10^(-19) C)(1.8 T))=3.77 \cdot 10^(-8)m`

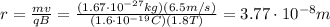
And now we can calculate the centripetal acceleration of the proton, which is given by

`a_c = (v^2)/(r)= ((6.5 m/s)^2)/(3.77\cdot 10^(-8)m)=1.12 \cdot 10^9 m/s^2`