Question

If the function f(x)=mx+b has an inverse function, which statement must be true

Answer 1

The things we know that are true based on this is that m does not equal 0 and the inverse function is f(x) =
`(x - b)/(m)`.

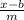We know that the slope is not 0, because there is no inverse function if this is the case.

Secondly, we can find the inverse function by switching f(x) and x and solving for the new f(x). The work for this is below.

f(x) = mx + b ----> switch f(x) and x

x = mf(x) + b ----> subtract b

x - b = mf(x) ----> divide by m

f(x) =
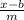`(x - b)/(m)`.

Answer 2

im pretty sure its
m=/0 because when m is 0 then f(x) does not depend on the value of x.
Hope this helped!