Answer: The correct option is (A)
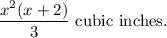
Step-by-step explanation: Given that a right pyramid with a square base has a base length of x inches and the height is two inches longer than the length of the base.
We are to select the correct expression that represents the volume of the pyramid in terms of x.
We know that
VOLUME of a right pyramid with base area 'b' square units and height 'h' units is given by
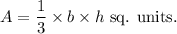
In the given square pyramid,
the base is a square with side length x inches, so the area of the base will be
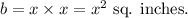
And, the height is 2 inches longer than the length of the base, so the height will be
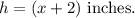
Therefore, the VOLUME of the regular pyramid is

Thus, the required volume is
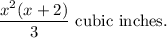
Option (A) is correct.