Question

A right pyramid with a square base has a base length of x inches, and the height is two inches longer than the length of the base. Which expression represents the volume in terms of x?

x^2(x+2)/3 cubic inches
x(x+2)/3 cubic inches
x^3/3+2 cubic inches
x^3+2/3 cubic inches

Answer 1

check the picture below.

Answer 2

Answer: The correct option is (A)
`(x^2(x+2))/(3)~\textup{cubic inches.}`

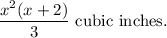
Step-by-step explanation: Given that a right pyramid with a square base has a base length of x inches and the height is two inches longer than the length of the base.

We are to select the correct expression that represents the volume of the pyramid in terms of x.

We know that

VOLUME of a right pyramid with base area 'b' square units and height 'h' units is given by

`A=(1)/(3)* b* h~\textup{sq. units.}`

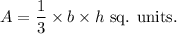
In the given square pyramid,

the base is a square with side length x inches, so the area of the base will be

`b=x* x=x^2~\textup{sq. inches.}`

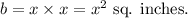
And, the height is 2 inches longer than the length of the base, so the height will be

`h=(x+2)~\textup{inches.}`

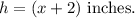
Therefore, the VOLUME of the regular pyramid is

`V=(1)/(3)* b* h=(1)/(3)* x^2* (x+2)=(x^2(x+2))/(3)~\textup{cubic inches}.`

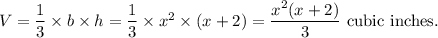
Thus, the required volume is

`(x^2(x+2))/(3)~\textup{cubic inches}.`

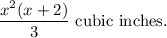
Option (A) is correct.